Yeah, yeah. I was just looking for the answer. Not really trying to prove why that had to be the answer. My maths education has stopped since high school. Just found it an interesting problem to tackle
| SudokuSolver Forum http://www.rcbroughton.co.uk/sudoku/forum/ |
|
| Recreational Maths http://www.rcbroughton.co.uk/sudoku/forum/viewtopic.php?f=17&t=21 |
Page 2 of 2 |
| Author: | Para [ Sun May 25, 2008 10:15 am ] |
| Post subject: | Re: Recreational Maths |
Yeah, yeah. I was just looking for the answer. Not really trying to prove why that had to be the answer. My maths education has stopped since high school. Just found it an interesting problem to tackle |
|
| Author: | udosuk [ Mon May 26, 2008 7:26 am ] |
| Post subject: | Re: Recreational Maths |
Okay, having received a little bit more of Maths education Hidden Text: Pretty easy compared to a typical Killer Sudoku, don't you think? |
|
| Author: | Glyn [ Mon May 26, 2008 6:56 pm ] |
| Post subject: | Re: Recreational Maths |
Of course at least 4 of the values must be sums:- Hidden Text: |
|
| Author: | udosuk [ Wed May 28, 2008 5:39 am ] |
| Post subject: | Re: Recreational Maths |
Glyn wrote: Of course at least 4 of the values must be sums:- Hidden Text: Following that line here is a different approach: Hidden Text: I posted some other similar challenges |
|
| Author: | udosuk [ Mon Jun 16, 2008 2:29 am ] |
| Post subject: | Re: Recreational Maths |
rcbroughton wrote: One of my very favourite Mathematical puzzles is one that my father showed to me about 20 years ago - and it was old, even then. If you haven't come across it before, it's a real gem. It just doens't look like you have enough information to make any headway but very rewarding when you crack it. 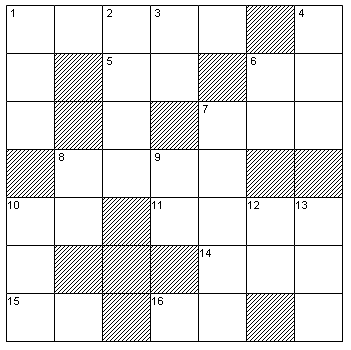 Code: Across 1 Area in square yards of the Paddock 5 Age of Martha, Squire Root’s aunt 6 Difference in yards between the length and the breadth of the Paddock 7 Number of Roods in the Paddock times 8 down 8 The year the Root family acquired the Paddock 10 Squire Root’s age 11 Year of Mary’s birth 14 Perimeter in yards of the Paddock 15 Cube of Squire Root’s walking speed 16 15 across minus 9 down Down 1 Value in shillings per rood of the Paddock 2 Square of the age of Squire Root’s mother-in-law 3 Age of Mary, Squire Root’s daughter 4 Value in pounds of the Paddock 6 Age of Ted, Squire Root’s son, who will be twice the age of his sister, Mary in 1945 7 Square of the breadth of the Paddock 8 Time in minutes it takes Squire Root to walk 1+1/3 times around the Paddock 9 10 down divided by 10 across 10 10 across multiplied by 9 down 12 Sum of the digits of 10 down plus 1 13 Number of years the paddock has been in the Root family Useful Information The Paddock is a rectangular plot of land The year is 1939 1 acre = 4840 square yards = 4 roods 1 mile = 1760 yards 1 pound = 20 shillings Finally worked out the solution. The solution: I believe the little typo in the "8 Down" clue (1+1/3=4/3 and 11/3=3+2/3 are very different Otherwise, quite enjoyable once you got everything worked out. |
|
| Author: | Bigtone53 [ Mon Oct 06, 2008 10:58 pm ] |
| Post subject: | Re: Recreational Maths |
udosuk, I think that I may have mentioned elsewhere my enthusiasm for Gardner, ever since I started seeing his Scientific American articles over 40 years ago. A real polymath (still apparently with us at 94). His interest in impromptu magic and the deep research into annotating things like Alice in Wonderland also touched nerves. A good man |
|
| Page 2 of 2 | All times are UTC |
| Powered by phpBB® Forum Software © phpBB Group https://www.phpbb.com/ |
|