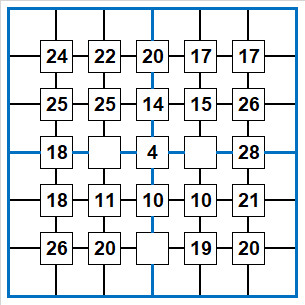
Clues are the totals of the 4 adjacent cells.
Nonets are normal, containing 1-9.
Numbers may repeat in clue totals, but only when some of the numbers are in different nonets.
Numbers may repeat in rows and columns.
1a. R34C34 = 4 = [1111]
1b. R23C23 = 25 contains 1 in R3C3 -> R2C23 + R3C2 = 24 = {789}, locked for upper-left nonet
1c. R45C23 = 11 contains 1 in R4C3 -> R4C2 + R5C23 = 10 = {235}, locked for lower-left nonet
1d. R45C45 = 10 contains 1 in R4C4 -> R4C5 + R5C45 = 9 = {234}, locked for lower-right nonet
1e. R45C34 = 10, R4C34 = [11] = 2 -> R5C34 = 8 = [53]
1f. R45C12 = 18, R45C2 = {23} = 5 -> R45C1 = 13 = {49/67}, no 8
1g. R45C56 = 21, R45C5 = {24} = 6 -> R45C6 = 15 = {69/78}, no 5
1h. R56C12 = 26, R5C2 = {23} -> R5C1 + R6C12 = 23,24 = {689/789}, no 4, 8,9 locked for lower-left nonet
1i. R23C34 = 14, R3C34 = [11] = 2 -> R2C34 = 12 = [75/84/93]
1j. R12C34 = 20, R2C34 = 12 -> R1C34 = 8 = {26/35}/[44], no 7,8,9
2. The four clues in upper-left nonet total 96 which includes R13C13 once, R13C2 + R2C13 twice and R2C2 four times
2a. Subtract 45 for R123C123 once; this leaves R13C2 + R2C13 + three times R2C2 = 51
2b. Subtract 24 for R2C23 + R3C2 (R3C3 has already been subtracted by step 2a); this leaves R1C2 + R2C1 + twice R2C2 = 27
2c. R1C2 + R2C1 + twice R2C2 = 27, R12C12 = 24 -> R2C2 = R1C1 + 3 -> R1C1 + R2C2 = [69] (cannot be [47] = 11 because R1C2 + R2C1 cannot total 13, cannot be [58] = 13 which clashes with R1C2 + R2C1 = 11 = {56}) -> R1C1 = 6, R2C2 = 9
2d. R12C12 = 24, R1C1 + R2C2 = [69] = 15 -> R1C2 + R2C1 = 9 = {45}, locked for upper-left nonet
2e. R12C23 = 22 with R1C2 from {45}, R1C3 from {23}, R2C2 = 9, R2C3 from {78} can only be [4297] -> R2C1 = 5, R3C12 = [38]
[I originally used ‘algebra’ for the lower-left nonet, but no need for that now with the corrected puzzle.]
3a. R34C12 = 18, R3C12 = [38] = 11 -> R4C12 = 7 = [43]
3b. R45C12 = 18, R4C12 = 7 -> R5C12 = 11 = [92]
3c. R56C12 = 26, R5C12 = 11 -> R6C12 = 15 = {78}, locked for lower-left nonet
3d. R56C23 = 20, R5C23 = [25] = 7 -> R6C23 = 13 = [76], R6C1 = 8
[There is no total for R56C34, so I’ll use my original ‘algebra’ for this step.]
4. The four clues in lower-right nonet total 70 which includes R46C46 once, R46C5 + R5C46 twice and R5C5 four times
4a. Subtract 45 for R456C456 once; this leaves R46C5 + R5C46 + three times R5C5 = 25
4b. Subtract 9 for R4C5 + R5C45 (R4C4 has already been subtracted by step 4a); this leaves R5C6 + R6C5 + twice R5C5 = 16
4c. R5C6 + R6C5 + twice R5C5 = 16, R56C56 = 20 -> R6C6 = R5C5 + 4 -> R5C5 + R6C6 = [26] (cannot be [48] = 12 because R5C6 + R6C5 cannot total 8)
4d. R5C6 + R6C6 = [26] = 8 -> R5C6 + R6C5 = 12 = [75]
4e. R45C56 = 21, R45C5 = [42] = 6, R5C6 = 7 -> R4C6 = 8, R6C4 = 9
5a. R34C56 = 28, R4C56 = [48] = 12 -> R3C56 = 16 = {79}, locked for upper-right nonet
5b. R23C34 = 14, R2C3 = 7, R3C34 = [11] = 2 -> R2C4 = 5
5c. R12C34 = 20, R1C3 = 2, R2C34 = [75] = 12 -> R1C4 = 6
5d. R23C56 = 26, R3C56 = {79} = 16 -> R2C56 = 10 = {28}, locked for upper-right nonet
5e. R12C45 = 17, R12C4 = [65] = 11 -> R12C5 = 6 = [42] -> R12C6 = [38]
5f. R23C45 = 15, R23C4 = [51] = 6, R2C5 = 2 -> R3C5 = 7, R3C6 = 9